반응형
1. 의사결정나무(Decision Tree)란?
- 의사결정나무는 머신러닝에서 자주 사용되는 알고리즘으로, 데이터를 분류하거나 회귀 분석을 할 때 활용됩니다.
- 마치 스무고개처럼 질문을 던지고 데이터를 분류하는 방식으로 작동하며, 이를 통해 예측 가능한 규칙들의 집합을 생성합니다.
- 의사결정나무는 범주형 데이터와 연속형 데이터 모두 예측이 가능하며, 트리 구조를 기반으로 학습합니다.

2. 의사결정나무 장점과 단점
1) 장점
- 해석이 쉬움 : 트리 구조가 직관적이므로, 다른 지도학습 기법에 비해 해석하기 용이합니다.
- 범주형 & 연속형 데이터 모두 처리 가능 : 분류 모델과 회귀 모델 모두 사용이 가능합니다.
- 비모수 모형 : 선형성, 정규성, 등분산성 등의 수학적 가정이 불필요합니다.
- 전처리가 비교적 쉬움 : 스케일링이 의사결정나무 알고리즘에 아무런 영향을 주지 않으므로, 스케일링을 할 필요가 없습니다.
2) 단점
- 과적합 위험 존재 : 훈련 데이터 위주의 분류가 이루어질 수 있어, 예측이 불안정할 수 있습니다.
- 작은 변화에 민감 : 데이터가 조금만 변경되어도 트리 구조가 크게 바뀔 수 있습니다.
- 성능 저하 가능성 : 다른 알고리즘보다 성능이 낮을 수 있습니다.
- 예측 어려움 : 분류 기준값의 경계선 주변의 자료에서는 오차가 클 수 있으며, 각 예측 변수의 효과를 파악하기 어려울 수 있습니다.
3. 의사결정나무 기본 개념
1) 트리 구조
- 루트 노드(Root Node) : 의사결정나무의 가장 상단에 있는 노드로, 최초 질문이 시작되는 지점입니다.
- 결정 노드(Decision Node) : 특정 기준에 따라 데이터를 분류하는 노드입니다.
- 리프 노드(Leaf Node) : 가장 하단에 있는 노드로, 분류 결과를 나타냅니다.
- 가지(Edge) : 노드와 노드를 연결해 주는 선을 의미합니다.
2) 데이터 분할 기준
(1) 지니 불순도(Gini impurity)
- 지니 불순도는 임의의 데이터가 잘못 분류될 확률을 의미합니다.
- 의사결정나무의 기준 매개변수의 기본값이 Gini이며, 지니 불순도를 계산하는 방법은 다음과 같습니다.
- 지니 불순도 = 1 - (음성 클래스 비율 ^ 2 + 양성 클래스 비율 ^ 2)

- 따라서 의사결정나무는 지니 불순도를 최소화하는 방향으로 데이터를 나누며, 부모 노드(parent node)와 자식 노드(child node)의 불순도 차이가 클수록 좋은 분할로 간주됩니다.
(2) 정보 이득(Information Gain)
- 부모 노드와 자식 노드의 불순도 차이를 정보 이득이라고 합니다.
- 의사결정나무는 정보 이득이 큰 방향으로 데이터를 나누는 것이 이상적입니다. 노드를 순수하게 나눌수록 정보 이득이 커집니다.
- 이때 사용하는 기준이 지니 불순도 외에도 엔트로피(Entropy) 불순도가 있습니다.
4. 의사결정나무 실습
- scikit-learn에서 제공하는 붓꽃 데이터를 활용하여 실습을 진행해 보겠습니다.
1) 데이터 불러오기
# 관련 모듈 불러오기
import pandas as pd
import matplotlib.pyplot as plt # 데이터 시각화
from sklearn.model_selection import train_test_split # 데이터 분할
from sklearn.tree import DecisionTreeClassifier, plot_tree # 의사결정나무
from sklearn.datasets import load_iris # iris 데이터셋
# 데이터 불러오기
iris = load_iris()
# 데이터프레임 변환
df = pd.DataFrame(iris.data, columns = iris.feature_names)
df["target"] = iris.target
# 데이터 확인
df.head()- iris 데이터셋을 불러온 후, target을 별도 설정하여 종속변수로 지정해 줍니다.
2) 데이터 정보 확인
# 데이터의 행과 열 개수 파악
df.shape
# 데이터 전체 정보 파악
df.info()
# 데이터 통계 파악
df.describe()
# target의 종류 및 개수 확인
df["target"].value_counts()
- iris 데이터셋 정보:
- sepal length : 꽃받침 길이
- sepal width : 꽃받침 폭
- petal length : 꽃잎 길이
- petal width : 꽃잎 폭
- target: 0 - setosa(붓꽃) / 1 - versicolor (무지개색의 붓꽃) / 2 - virginica(잡초)
3) 데이터 전처리
# 데이터 분할
x = df.drop("target", axis = 1) # 독립변수
y = df["target"] # 종속변수
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.2, stratify = y,
random_state = 22)
- 의사결정나무는 스케일링이 필요하지 않으므로 별도의 전처리 과정 없이 진행할 수 있습니다.
4) 의사결정나무 모델 생성 및 평가
# 모델 생성
dt = DecisionTreeClassifier(random_state = 22)
dt.fit(x_train, y_train)
# 모델 평가
print(dt.score(x_train, y_train)) # 훈련 데이터 정확도
print(dt.score(x_test, y_test)) # 테스트 데이터 정확도
- 모델 평가 결과 값을 보면 훈련 데이터는 1.0이며, 테스트 데이터는 0.9333333333으로 나타났습니다. 이러한 결과를 보아 과대적합을 의심해 볼 수 있습니다.
5) 의사결정나무 시각화
max_depth : 루트 노드를 제외하고 표현할 깊이의 수
filled : 클래스에 맞게 색을 칠함(False일 경우에는 흰 배경으로 나타남)
feature_names : 특성의 이름을 전달함
# 데이터 시각화
plt.figure(figsize = (6, 7))
plot_tree(dt, max_depth = 3, filled = True, feature_names = iris.feature_names)
plt.show()
5. 의사결정나무 가지치기
- 모델 평가의 값을 보면, 과대적합을 의심할 수 있습니다.
- 이처럼 깊이에 제한을 두지 않고 끝까지 자라나는 트리를 그리면 과대적합 모델이 되어 일반화하기가 어렵게 됩니다. 이에 트리의 성장을 제한하는 가지치기를 활용하여 트리의 최대 깊이를 지정할 수 있습니다.
1) 가지치기 후 모델 생성 & 평가
# max_depth를 통해 깊이 제한
dt = DecisionTreeClassifier(max_depth = 3, random_state = 22)
# 모델 생성
dt.fit(x_train, y_train)
# 모델 평가
print(dt.score(x_train, y_train))
print(dt.score(x_test, y_test))
- 처음에 진행한 의사결정나무와 비교했을 때, 정확도 차이가 줄어든 것을 확인할 수 있습니다.
- 가지치기를 수행하면, 트리의 복잡도가 줄어들어 일반화 성능이 향상될 수 있습니다.
2) 가지치기한 트리 시각화
# 가지치기한 트리 시각화
plt.figure(figsize = (5, 7))
plot_tree(dt, filled = True, feature_names = iris.feature_names)
plt.show()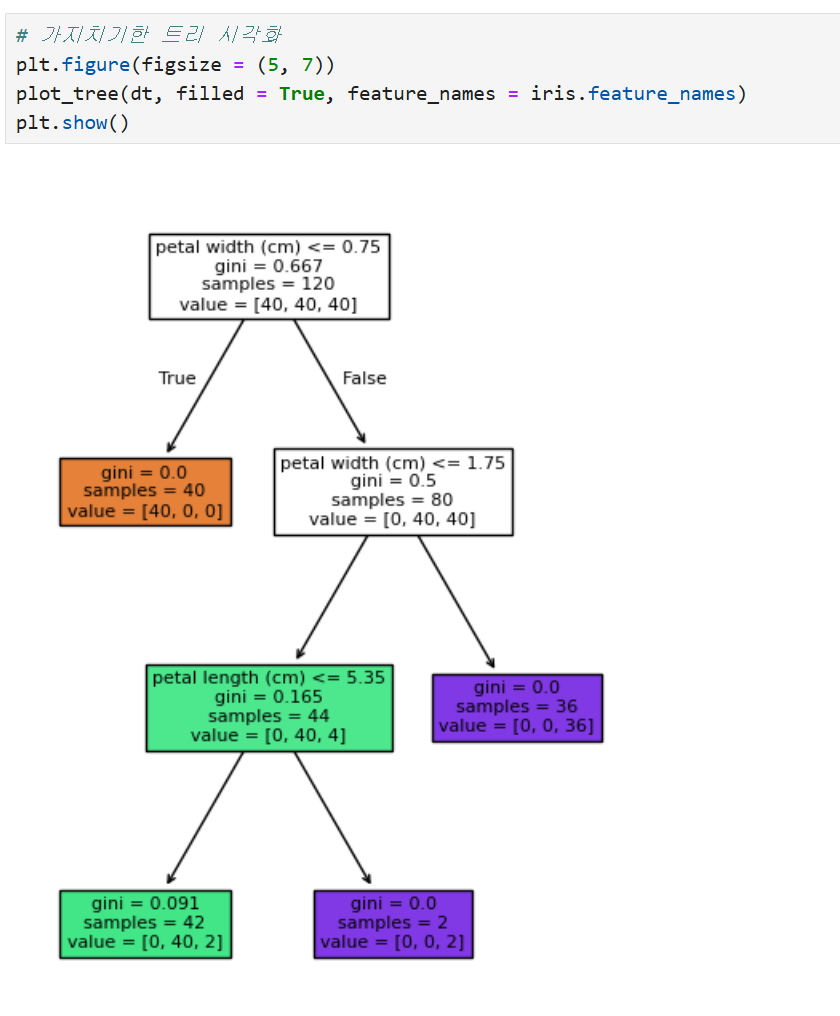
의사결정나무는 직관적인고 강력한 머신러닝 모델입니다. 하지만 과적합 방지를 위해서는 가지치기 및 하이퍼파라미터 튜닝이 필수입니다. 다음 글에서는 의사결정나무 시각화 해석 방법을 다뤄보겠습니다.
감사합니다:-)
'데이터 분석 관련' 카테고리의 다른 글
| 단층신경망(Single-Layer Perceptron)이란? 개념부터 실습까지! (0) | 2025.03.30 |
|---|---|
| 의사결정나무 시각화, 어떻게 읽어야 할까? - 의사결정나무 시각화 해석하는 방법 (0) | 2025.03.12 |
| 파이썬: mutable과 immutable 구분하기 / PyCharm 활용 (0) | 2025.03.05 |
| [통계 개념] 정규분포, 첨도와 왜도 알아보기 (0) | 2025.02.25 |
| pandas(6) : 날짜 데이터 변환 및 변환 오류 / 주피터노트북 (0) | 2025.02.19 |


